Regular Expression to Automaton
When the converter starts up, all that appears initially are two states (one initial and one final) with a transition. The transition between them contains the regular expression that we are trying to convert.
The critical idea of the converter is that at each stage of the conversion one has a valid machine where some transitions may happen to be regular expressions. Each regular expression may be recursively broken into smaller parts. The conversion is finished when the only transitions have only single (or zero) alphabet symbols on them.
There are four types of reductions that can be done on a regular expression:
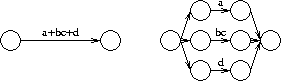 Transitions are first broken according to the or symbol (+). For example, the expression a+bc+d can be broken into three subexpressions a, bc and d. An example of such a breakup is shown above.
Transitions are first broken according to the or symbol (+). For example, the expression a+bc+d can be broken into three subexpressions a, bc and d. An example of such a breakup is shown above.
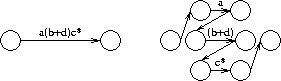 Transitions that cannot be broken across ors are then broken across concatenations. For example, a(b+d)c* would be broken into the three subexpressions a, (b+d), c* as shown above.
Transitions that cannot be broken across ors are then broken across concatenations. For example, a(b+d)c* would be broken into the three subexpressions a, (b+d), c* as shown above.
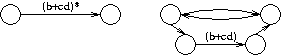 If the transition does not break across either concatenation or or, then it may be a Kleene star (*) term, of the form a* or (b+cd)* (shown above) or something in that vein. In this case, the user effects the removal of the Klein star.
If the transition does not break across either concatenation or or, then it may be a Kleene star (*) term, of the form a* or (b+cd)* (shown above) or something in that vein. In this case, the user effects the removal of the Klein star.
Lastly, if a regular expression is of the form (...), then the parentheses are simply removed from the transition.
The user interacts with the system in this way:
- In the first stage of the breakup, one uses the "de-expressionify" tool (
 ) to select a transition with a regular expression that can be broken down. If a particular transition cannot be broken down further, the user is gently chastised.
) to select a transition with a regular expression that can be broken down. If a particular transition cannot be broken down further, the user is gently chastised.
- If this is a reduction that requires additional lambda transitions, the user may add them with the transition tool (
 ). A small message in the upper portion of the window will report how many transitions remain to add. If the user makes an error in the process of adding the transitions, the user will immediately receive a message to that effect. When all required transitions are added, the reduction is considered complete.
). A small message in the upper portion of the window will report how many transitions remain to add. If the user makes an error in the process of adding the transitions, the user will immediately receive a message to that effect. When all required transitions are added, the reduction is considered complete.
- Steps 1 and 2 are repeated until there are no more transitions that can be "de-expressionified."
At any time, the user may press "Do Step" to complete the current RE reduction; if no RE reduction is in progress, this will choose a transition that remains to be reduced, and reduce it. "Do All" will complete the building of the automaton.
When the automaton is fully built, as with similar conversion operations the user has the option of placing the NFA in its own window with the "Export" button.
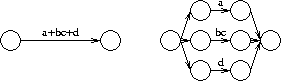 Transitions are first broken according to the or symbol (+). For example, the expression a+bc+d can be broken into three subexpressions a, bc and d. An example of such a breakup is shown above.
Transitions are first broken according to the or symbol (+). For example, the expression a+bc+d can be broken into three subexpressions a, bc and d. An example of such a breakup is shown above.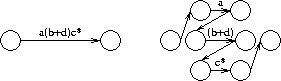 Transitions that cannot be broken across
Transitions that cannot be broken across 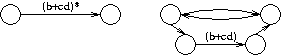 If the transition does not break across either concatenation or
If the transition does not break across either concatenation or