MPIViz Manual

INTRODUCTION

In parallel computing, a single task is divided into smaller subtasks and then these subtasks are distributed among numerous processing units. This results in reduce execution time. While execution these subtasks often need to communicate with each other. On any typical cluster this communication is done by sockets. However it is difficult to implement sockets each time you want to transfer data from one processor to another. MPI is solution for this problem. Message Passing Interface (MPI) is both a computer specification and is an implementation that allows many computers to communicate with one another. Under the hood MPI uses sockets for data transfer.

There are numerous network topologies which can be used to connect various processing units in any cluster e.g. Ring, Tree, Mesh, Taurus and Hypercube. Moreover MPI communications are also not simply point to point. They can be as complex as all-to-all where each process has some unique data and all the processors must get all these data pieces. In these situations it is imperative for any MPI library to effectively use network topology and intrinsic requirements of communication pattern to do the job efficiently with least network congestion. For the same purpose, algorithms used by these MPI libraries differ enormously with network topology and communication needs.

In this visualization tool we show how various MPI functions are implemented over a hypercube topology. Hyper is very efficient network topology and is frequently used in huge clusters.

BACKGROUND

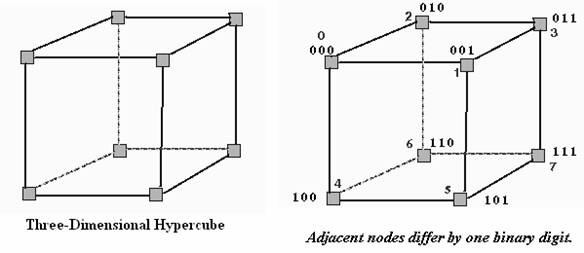
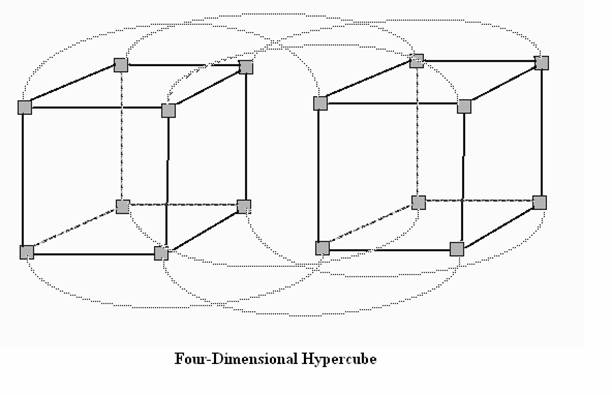
HYPERCUBE

In geometry, a hypercube is an n-dimensional analogue of a square (n = 2) and a cube (n = 3). It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, at right angles to each other.

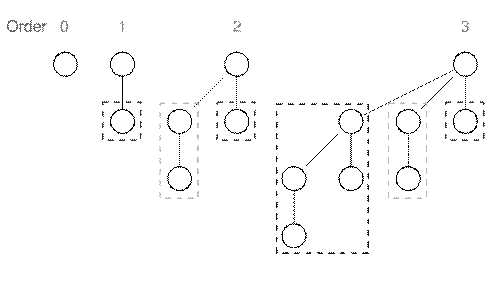
BINOMIAL TREE

1. A binomial tree of order 0 is a single node

2. A binomial tree of order k has a root node whose children are roots of binomial trees of orders k-1, k-2, ..., 2, 1, 0 (in this order).

Binomial trees of order 0 to 3: Each tree has a root node with subtrees of all lower ordered binomial trees, which have been highlighted. For example, the order 3 binomial tree is connected to an order 2, 1, and 0(highlighted as blue, green and red respectively) binomial tree. Source: wikipedia

Also note that from any node of hyper cube it is possible to super impose a binomial tree of order n (containing all the nodes of hypercube) where n is the dimension of hypercube. Thus all MPI algorithm implemented for hypercube topology actually use binomial tree. The root of the binomial tree is chosen as per need.

MPI COMMANDS

1. Broadcast: Root node has message which must be delivered to all the other nodes in the cluster.

2. Gather: Every node has some data which must be collected and transferred to root node.

3. Scatter: Root node has some data which must be broken into pieces and delivered to all the nodes in the cluster correspondingly.

4. Reduce: Same as gather but data pieces gathered are reduced to one piece by any aggregating operation (e.g. sum or multiplication etc).

TOOL DOCUMENTATION:

MPIViz is a visualization tool for commonly used MPI Commands. The interface for the tool looks as below:

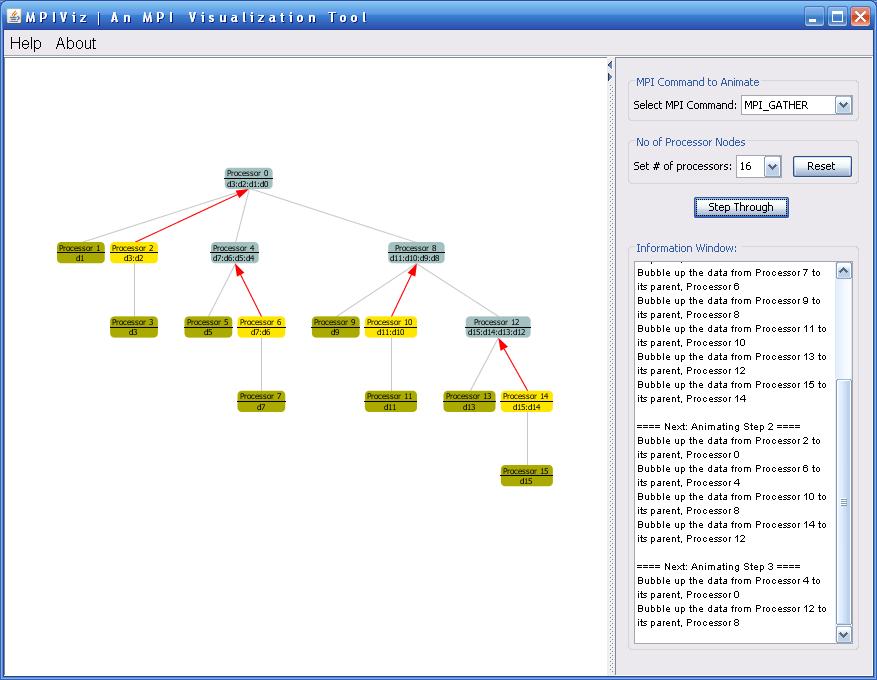
To view an animation, select the MPI Command you want to view from the drop down box on the right side of the pane. The processors are laid out as a Binomial tree on the left hand side of the pane. You can select and redraw a layout with different number of processors.

If you hover the mouse over the nodes in the tree will display contents of the node in the status bar. You can step through the algorithm using the 'Step Through' button. The underlying network is considered to be a hypercube network, which can be represented as a binomial tree.

Step through the animation one time step at a time to understand the algorithm.

Pay careful attention to the data in the processor nodes at every step and the processors involved.

Processors have been color coded to hint at the state they are in at every time step.

RECENT CHANGES:

• Get rid of drop down box and button combo. Drop down box should be enough. E.g. Remove “Set MPI Command” Button. Selection in drop down box should be enough. Also replace “reset and redraw” button. Replace it with reset button (with same functionality). However decouple it with “# of processor” drop down box. Selection of any element in drop down box should be enough to trigger all the changes which are associated with buttons now.
• We need to document pan and zoom capabilities of AV. Right drag pans and left drag zooms etc.
• It seems AV finishes a step too soon. Last frame make all the nodes’ color as finished node.
• Disable step button at finish.
• Change of behavior: In previous version, description of the MPI command was removed from the History window, so user could not refer to it while running the animation. Now the description is maintained within the history window.
• Inserted a brief message in the history window for MPI_REDUCE, MPI_SCATTER, MPI_GATHER and MPI_ALL_REDUCE about the ":" separator between data elements. It means that data is in different memory locations.
• A legend of the colors representing the states of a Processor during the runtime of MPI algorithm has been added to the documentation. It is not added to the visualization itself as the use of different colors is pretty intuitive.
• Bug Fix: Clicking on processor nodes displaces the entire tree from the center of the frame.

Algorithm and Description has been referenced from Introduction to Parallel Computing, 2nd Edition, by Ananth Grama; Anshul Gupta; George Karypis; Vipin Kumar, from Addison-Wesley.